Triangle
| Triangle | |
|---|---|
 |
|
| Edges and vertices | 3 |
| Schläfli symbol | {3} (for equilateral) |
| Area | various methods; see below |
A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called vertices, are zero-dimensional points while the sides connecting them, also called edges, are one-dimensional line segments. A triangle has three internal angles, each one bounded by a pair of adjacent edges; the sum of angles of a triangle always equals a straight angle (180 degrees or π radians). The triangle is a plane figure and its interior is a planar region. Sometimes an arbitrary edge is chosen to be the base, in which case the opposite vertex is called the apex; the shortest segment between base and apex is the height. The area of a triangle equals one-half the product of height and base length.
In Euclidean geometry, any two points determine a unique line segment situated within a unique straight line, and any three points that do not all lie on the same straight line determine a unique triangle situated within a unique flat plane. More generally, four points in three-dimensional Euclidean space determine a tetrahedron.
In non-Euclidean geometries, three "straight" segments (having zero curvature) also determine a triangle, for instance a spherical triangle or hyperbolic triangle. A geodesic triangle is a region of a general two-dimensional surface enclosed by three sides which are straight relative to the surface (geodesics). A curvilinear triangle is a shape with three curved sides, for instance a circular triangle with circular-arc sides. This article is about straight-sided triangles in Euclidean geometry, except where otherwise noted.
Triangles are classified into different types based on their angles and the lengths of their sides. Relations between angles and side lengths are a major focus of trigonometry. In particular, the sine, cosine, and tangent functions relate side lengths and angles in right triangles.
Definition, terminology, and types
A triangle is a figure consisting of three line segments, each of whose endpoints are connected.[1] This forms a polygon with three sides and three angles. The terminology for categorizing triangles is more than two thousand years old, having been defined in Book One of Euclid's Elements.[2] The names used for modern classification are either a direct transliteration of Euclid's Greek or their Latin translations.
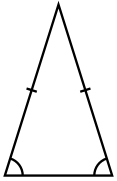
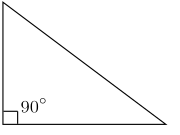
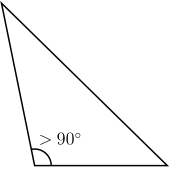
Triangles have many types based on the length of the sides and on the angles. A triangle whose sides are all the same length is an equilateral triangle,[3] a triangle with two sides having the same length is an isosceles triangle,[4][a] and a triangle with three different-length sides is a scalene triangle.[7] A triangle in which one of the angles is a right angle is a right triangle, a triangle in which all of its angles are less than that angle is an acute triangle, and a triangle in which one of it angles is greater than that angle is an obtuse triangle.[8] These definitions date back at least to Euclid.[9]
-
Scalene triangle